[an error occurred while processing this directive]

Lottery Math

Okay, so it's Saturday night and you're tuned to the lottery show and clutching the ticket that could change your life. The machine is loaded with 49 red and blue balls, and you need to match 6 of them. The drum rolls, the spinner spins, the first ball bounces down the chute, and.... What are the odds that it has one of the numbers you've picked?

Well, since there are 49 balls, then the chance of getting any one of the 6 is 6 divided by 49. Mathematicians like to write this as:

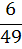
If by great good fortune you do make this first ball, then there are 48 balls remaining in the machine, only 5 of which are any good to you. So the chance of getting the second one is:

Combining this with your first ball means that the chances of matching the first two numbers is

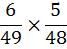
... which works out to about 1 in 78.

Of course you still have to match 4 more numbers, which are hiding among the 47 balls left in the machine. So we just continue multiplying all the way down....

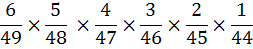
...which equals exactly 1 over 13,983,816.

But what if you're playing a different lottery? One that has a different number of balls and numbers to choose from? We can use the same downward multiplying. There's even a formula for it.

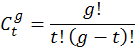
...where C is the total number of possible combinations, g is the size of the group (the "49" in 6/49) and t is the subgroup or ticket size (the "6"). (The ! stands for factorial and means to multiply that number by all the whole numbers below it. You knew that.)

So for 6/49 ticket combinations, we plug the numbers into the formula, like so:

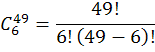
This reduces to....

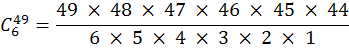
...and still further to...

...which equals 13,983,816

(Since it doesn't matter what order those 6 balls drop out of the machine, we have to divide out the number of ways they can be rearranged, which is 6! or 720. You also knew that.)

So there you have it: your chance of becoming a millionaire is slightly better than 1 in 14 million. Maybe not as steep as the Mega Millions or that daunting Italian Lotto, but steep enough. I am more likely to guess your phone number.

"But," you might ask (you didn't ask, but you might), "what about the smaller prizes?" Finding the odds for winning a 3/6 merely takes more of the same calculation.

Out of the 6 numbers you pick, any 3 of them could make a 3/6. To learn how many ways they can do it, we plug the values into the formula to get:

If 3 of your numbers do match the winning draw, then your ticket will also contain 3 losing numbers. These will be from the 43 remaining numbers that weren't drawn. And the way these can be formed can also be found by the combination formula:

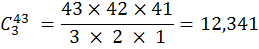
Multiply this by the number of possible winners, and we get 12,341 × 20 or 246,820 different ways to win $10 on the 6/49. To get the odds, divide this number into the total number of possible 6/49 combinations....

This can be rounded to 1 in 57.

Putting it all together, the formula for finding the Odds O of matching m numbers in a ticket of size t within a group of g numbers is:

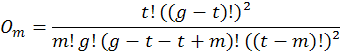
There's still the bonus number to figure. There are 258 ways to match 5 numbers on the 6/49. The bonus number is drawn from the 43 losing numbers, making 258/43 or 6 ways to make the bonus. Divide 6 into 13,983,816 and you get 1 chance in 2,330,636. But if smaller matches are eligible (such as the 2/6 in the Canadian 6/49) then you have more guesses at it. The formula for getting the bonus for m matches is:

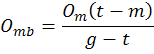
In the case of the 2/6, that works out to:

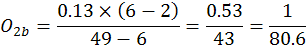
Again, I round this to 1 in 81.

The Powerball is even easier to calculate. Since it's drawn separately, you have only one chance to make it. Simply divide the original odds by the size of the powerball to get your new odds. For example, the Mega Millions offers 5 numbers out of 75, giving 17,259,390 different combinations. But that 15-number powerball puts the jackpot into a vanishingly small chance of 1 in 258,890,850.

Of course the odds are only half the story. The other, critical, half is the payout. And it's the payout times the odds which determine whether the game is worth playing. So if a ticket costs a dollar and the odds against winning are 10 million to one but the jackpot is $20 million, then you will make a profit—if you live long enough.

However, not even governments are that crazy. They consistently set the payout to be much lower than the odds. For example, if you were to buy every possible ticket on the BC49, you would win:

Match	Winners	Prize	Pays out
6/6	1	$2,000,000	$2,000,000
5/6+	6	$75,000	$450,000
5/6	252	$750	$189,000
4/6	13,545	$75	$1,015,875
3/6	246,820	$10	$2,468,200
2/6+	172,200	$5	$861,000
Total	432,824		$6,984,075

So you would buy slightly less than 14 million tickets to win slightly less than 7 million dollars.

Unlike the BC49 which has a fixed payout, most lottery companies use a parimutuel system in which the winnings are split among the players. The BC Lottery Corporation's Lotto 6/49 Game Conditions handbook explains how they pay out the prizes from every $3 ticket they sell:

After each draw, ILC allocates for the payment of prizes $1.41 for every play recorded on the computer system of any of its Regional Marketing Organizations for that draw to prize funds.

So it doesn't matter how many tickets you buy. The lottery company skims off 53% of the take and divvies the rest among the lucky few. And the higher the prize pool climbs, the more players are lured into the game, and the more ways the pot gets split. Seasoned gamblers call this playing against yourself.

But you don't have to take my word for it. There are two ways you can check my math:

1. The hard way
2. The easy way

[an error occurred while processing this directive]

Back to Contents